Neural Networks Art: Solving Problems with Multiple Solutions and New Teaching Algorithm
Abstract
A new discrete neural networks adaptive resonance theory (ART), which allows solving problems with multiple solutions, is developed. New algorithms neural networks teaching ART to prevent degradation and reproduction classes at training noisy input data is developed. Proposed learning algorithms discrete ART networks, allowing obtaining different classification methods of input.
1. PROBLEM FORMULATION AND ANALYSIS OF THE LITERATURE
The human brain processes information flows continuously from the external environment. However, it can modify and update the stored images, and create new, without destroying what previously memorized. Thus it differs significantly from the majority of neural networks as neural networks (NN), trained by back propagation, genetic algorithms, in bidirectional associative memory, Hopfield networks, etc. very often a new way of learning, situation or association significantly distorts or even destroys the fruits of prior learning, requiring a change in a significant part of weights of connections or complete ret raining of the network [1-4]. Impossibility of using the specified NN solve the problem of stability-plasticity, that is a problem of perception and memorization of new information without loss or distortion of existing, was one of the main reasons for the development of fundamentally new configurations of neural networks. Examples of such networks are neural networks, derived from the adaptive resonance theory (ART), developed by Carpenter and Grossberg [5, 6]. ART neural network classifies the input image to one of the known classes, if it is sufficiently similar to or resonates with the prototype of this class. After you have found a prototype with some accuracy given by the special parameter similarity corresponds to the input image, it is modified to be more like the presented image. When the input image was not like any of the existing prototypes, then it is based on a new class. This is possible thanks to the fact that the network has a significant number of unallocated redundant or elements which are not used as long as it is not necessary (if no unassigned elements, the input image is not network response). Thus, new images can create new classes, but did not distort the stored information.
It is developed a number of neural network based on adaptive resonance theory [7-11]. However, these neural networks have significant disadvantages: NN adaptive learning resonance theory (ART) often leads to degradation, and reproduction classes receive a unique solution, even in those cases where there are two or more possible and equivalent solutions, the results depend on the training images in order training sequence, etc.
This requires solving the fundamental problem - the architecture and algorithms to improve the functioning of the ART NN. In particular, it is necessary to develop the theoretical foundations of the ART NN with a new architecture and new learning algorithms.
In this paper we consider the most widely used single-module neural network ART-1, proposed to binary input images or vectors. Basic network architecture shown in Fig. 1 in phantom includes three groups of neurons: field F1 input processing neurons, consists of two layers of elements, recognition layer Y- neurons and control neurons R, G1, G2 (Fig. 1).
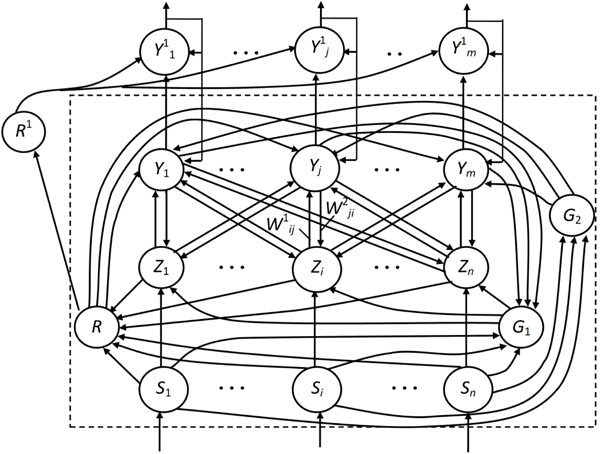
Architecture Neural Network ART.
Field F1 consists of two layers – input layer S-elements and the interface layer Z-elements. The input layer receives the image requirements and transmit the information received interface layer neurons and manage neurons R, G1, and G2. Each element of interface layer is associated with each element discriminating layer Y two kinds of weighted connections. Signals from the interface layer to layer Y transferred to a bottom-up connections with weights , and from discriminating layer to the interface – bonds with weights . Due to a large number of bonds in Fig. 1 shows only one pair symbol bonds with weights between interface and recognizing layers of elements.
Most of the connections shown in Fig. 1 are excitatory: from input layer S- elements to neurons R, G1, G2 and Z-layer, from neurons G1, G2 respectively to neurons layers Z and Y. Inhibitory signals are transmitted multiple links from the interface elements to R-neuron and from Y-neurons to element G1. All communications network ART-1 transmit only binary signals 0 or 1.
Each element in the interface or Y-layer neural network ART-1 has three input sources. Arbitrary interface element can receive signals from element Si input layer, from elements Y-layer and from neuron G1. Similarly, the element can receive signals from the interface elements, neurons R and G2. To translate the interface neurons layers or recognizing neurons layers in the active state, you must have two sources of input single excitation signals. Since each of the neurons is considered three possible signal sources, the condition of excitation of these neurons has been called " rules two of three".
Layer Y appears as layer of competing neurons. In steady-state conditions, each element recognizing layer located in one of three states:
- active (output signal neuron Yj equal "1");
- inactive ( but neuron may compete);
- braked ( and neuron not allowed to compete upon presentation of the current input image).
In the initial state neurons R, G1, G2 and the input layer S have zero output signals. at receipt on inputs S-elements binary components the displaying images some of them, received a single input signals, becomes to excited state (Uout = 1). Exciting signals from the outputs of these neurons transform to the state "1" neurons G1, G2, as well as supplied to respective inputs of the interface layer neurons. Interface layer neurons, which received the unit signals from neurons of the input layer and element G1, by the rule two of the three transferred to the active state and send their unit excitatory signals on relations with weights to the inputs of neurons Yj recognizing layer. Recognizing layer neurons transferred to the active state by rule two of the three, receiving excitatory signals not only from the elements of the interface layer, but from the element G2. Output signals active Y- neurons determined by the ratio
and satisfy condition: .
Then in Y-layer recognizing neurons occurs lateral process of selection single neuron with the highest output signal. All neurons Y-layer, besides winning YJ, transferred to inactive status "0" (), and the winning neuron – to a state with a single output. Single signal winning Y- neuron retards managing neuron G1, and also comes with on relations with weights to the inputs of the elements of the interface layer. Since the elements of the interface layer conform to the rule two of the three, then in the absence of the excitation signal from the neuron G1 in an active state remain only those interface elements, which receiving unit signals from the element of the input layer, and from winning YJ-neuron recognizing layer. Braking signals from active elements of the interface layer is applied to the inputs R-element, which receives also excitatory signals from the input layer neurons. With the help of R-element calculated value of parameter similarity p between the input image and image, stored in the weights of winning neuron connections:
where - norm of the vector ; - vector output signals, respectively Z- and S-layer elements.
If the calculated similarity value indicates coincidence with a given accuracy input and stored in the memory image, then the network resonance occurs. In this case on the output R-element will be zero output signal, and will be training weights winning neuron connections. When parameter value is less than the similarities preassigned on the output control R-element single signal appears, which victory Y-neuron braked () and actually deprived of the opportunity participate in competitions upon presentation of the current image. Then in Y-layer selects the new winning neuron. If the input image was not like none of the stored, then all distributed Y-neurons, eventually, are inhibited, and the winner becomes undistributed Y-element, who remembers in his weights new image.
Neural network ART-1 training is usually done using a fast learning algorithm [9, 12].
Fast Algorithm for training the neural network ART-1
The algorithm adopted such designations: Sk – n-measured input vector, k = 1, …, q;
q – number of input vectors;
n-measured vector of output signals of interface elements layer;
norm of vector Х;
р – parameter of likeness between an entrance vector and vector, kept in the scales of connections of winning neuron Y-layer; range of legitimate values of parameter: 0 < p < 1;
– weight of connection from an element Zi (i = 1, …, n) to the element Yj (j = 1, …, m); range of legitimate initial values recommended initial value: all calculations are executed taking into account the use K-value signals;
L – constant, excelling unit; recommended value: L = 2;
– weight of connection from an element Yj to the element Zi; recommended initial value.
Step 1. The first step is initializing parameters L, p and weights of connections from an interface layer to a weekend, and connections (i = 1, …, n; j = 1, …, m) from a weekend layer to the interface.
Step 2. The terms of stop are analyzed, and while they are not executed, steps 3 – 14 of algorithm will be realized.
Step 3. For every teaching entrance vector Sk (k = 1, …, q) are executed steps 4 – 13.
Step 4. Set zero signals of all recognizing elements of weekend Y-layer:
By an entrance vector Sk activating S-elements of input layer:
Step 5. The norm of output signals vector neurons of entrance layer is calculated:
Step 6. For the elements of interface layer entrance and output signals are formed:
Step 7. Settles accounts for output signal of every not brakes Yneuron:
if
Step 8. While not found Y-neuron of output layer, weight vector of which in accordance with the specified value of likeness parameter of р corresponds an entrance vector Sk, are executed steps 9 – 12.
Step 9. In Y-layer ascertain a neuron YJ, meeting a condition
If such elements few, gets out an element with the smaller index. If , then all elements are put on the brakes and entrance image can not be classified or memorized.
Step 10. Calculating output signals Z-elements of interface layer with the use K-value boolean operations:
Step 11. The norm of output signals vector of interface layer is calculated:
Step 12. Checked up the condition of teaching possibility of the selected neuron YJ.
If that condition is not executed end element YJ is braked, i.e. . After it passing carried out to the step 8 of algorithm.
If condition of teaching neuron YJ possibility is executed and progressing to the next step of algorithm.
Step 13. Adapt oneself weight of connections of element YJ taking into account the use K-value signals:
, i = 1, …, n,
, i = 1, …, n.
Step 14. The conditions of stop are checked up.
The conditions of stop can be: absence changes of scales net , during an epoch, achievement of the specified number of epochs and so on.
Step 15. Stop.
II. NEW ALGORITHMS FOR TRAINING NEURAL NETWORKS ART-1 FOR NOISY INPUT
During practical calculations revealed deficiencies fast learning algorithm NN ART-1, do not allow to use them effectively in real systems management and recognition, where the original data are noisy. In noisy input image fast training of the neural network algorithm can lead to degradation and reproduction classes, that is, the learning algorithm becomes inoperative. Demonstrate this lack of a specific example of a learning neural network ART-1.
Example 1. Suppose you want by using a neural network divided into two classes set of vectors:
Classification mentioned vectors can be performed in many ways. One of the most suggests itself - assigned to the first class of vectors, to the second class - vectors i.e. to build classes of vectors, differing from each other by not more than two components. These classes of vectors can be viewed as classes, which obtained by the impact of noise of vectors, resulting which in the vectors lost by one unit component. Let's try to get this classification using neural network ART-1. Let us take a network with parameters: m = 8 – number Y-neurons in discriminating network layer; n = 8 – number of neurons in the input layer of the network; р = 0,75 – similarity parameter; selected such numeric values based on the fact, that the vectors ; , in each class differ from each other by not more than two components, and the parameter of similarity is calculated using only single component vectors; - initial weights values of connections ; = 1 - initial weights values of connections
During training the neural network obtained the following results.
Presentation the neural network of the first vector and calculation the equilibrium weights of connections by the formulas (1) leads to the following weight matrix:
,
Analyzing example shows, that to determine the number of selected classes of input vectors rather one of the matrices , weights of connections, so in the future will only use a matrix of weights connections as a more informative.
Consistent presentation of the neural network of the following four vectors and calculation of the equilibrium weights of connections will result to following results. Presentation of the neural network training vector leads to, that in the first column of the matrix and the first row of the matrix there will be only three non-zero coefficient. Therefore, when the similarity parameter equal 0,75, subsequent training the neural network by vector cause the distribution one more recognizing Y -neuron. Further training neural network by vectors require the allocation of two more neurons from discriminating layer neural network. As a result, the matrix weighting coefficients connections between layers interface and recognizing neurons will have the form:
It is easy to verify that subsequent submission to the input of the neural network as a vector as well as vectors does not lead to a change in the first four columns of the matrix and the first four rows of the matrix Consistent presentation of the neural network of the following four vectors and calculation of the equilibrium weights of connections results in the release of four other neurons of the neural network from recognizes layer. As a result, the matrix weighting coefficients connections between layers of interface and recognition will be the following:
Thus, the analysis of the solution shows an example that the network ART-1 during training can not share a set of vectors into two classes, because it is reproduction classes. Vectors which could become the reference vectors of the two classes degraded in the process of presenting the following vectors, which leads to duplication of classes.
Failure to solving the problem of classification of the set of vectors associated with features of the architecture and neural network learning algorithm ART-1. First, the network connections in the weights of a neuron remembers recognizing the intersection of binary input vectors. Second, the proximity of binary vectors is defined by using parameter similarity, taking into account only single elements compared vectors. In the analyzed example intersection of set binary vectors and set of vectors give the vector with all zero components:
Thus, at the crossing of considered sets of vectors completely lost the information about the individual components of the binary vectors. Storing information in the form of crossing of the input binary vectors or an image in a neural network also leads to loss of information. For small values of similarity parameter may be lost most the information about classified or recognizable images. In this regard, there is an idea about memorizing information as a union, and not crossing binary images or vectors. In this case, in this example we have:
Remembering two vectors results in weight matrices connections with which could correctly classified all of the input image, if after the presentation of input vectors there was no adaptation of neural weights, change it memory.
However, remembering association binary vectors without a teacher also has its drawbacks, since can easily appear matrix of weights connections, having in their respective columns (matrix ) or rows (matrix ) for distributed Y-neurons minimum number of zero elements or even not having them at all. Therefore, when memorizing the combining binary vectors needed correction the work of algorithm or participating teacher.
Examples of successful use at training a neural network crossing or union of the input images indicate to the fact, that, apparently, may be prepared learning images also with using a combination of these operations, as well as using other operations on binary sets.
Thus, we can conclude, that adapting the weights of network connections in the form, wherein it is used in a neural network ART-1, is the lack of the network. The disadvantage, as shown by the above example, also may be the lack of teacher. Similar problems also arise in training the continuous NN ART.
Thus, the adaptation of weights of distributed recognizing communications Y-neurons net in the form, wherein it is used in the network ART-1, often fails to solve even trivial tasks of classification and training, then there is a significant lack of the network.
Moreover:
- final result of learning discrete network ART may depend on presentation of a sequence images;
- no training mode networks with teacher, that restricts the class solved by neural network problems classification and recognition.
To prevent degradation and reproduction classes, that is, for the correct and stable operation of the modules on based of neural network ART-1, proposed ban adaptation weights of connections of distributed recognition neurons. For this, at step 11 learning algorithm adaptation of connections weights of recognizing elements produced only, if these neurons were distributed earlier. Otherwise - weight relationships recognition elements not adapted. With this algorithm, the set of training M vectors, if they are served in the order, wherein they recorded in the set, is divided into two classes - to the first class relate vectors , to the second class - vectors that is, it turns out the most natural classification vectors. However, if the order of training vectors changes, for example, vectors in their subsets not subject to the net first, then changed also classification of the vectors.
III. TRAINING ALGORITHMS OF NEURAL NETWORK ART-1 WITHOUT ADAPTATION WEIGHTS OF CONNECTIONS DISTRIBUTED RECOGNITION NEURONS
General lack of different systems classification using a variety of neural networks or other approaches or methods consists in, that it turns out only one classification, due to the method of teaching or raised by teachers. At the same time, when there N various objects, it is possible to obtain . Polar cases of these classifications: one class contains all the objects; each of the N classes contains one object. At N = 10 number of possible ways of classifying exceeds 1000. Therefore require different approaches to select the best classification. One of these approaches may be specifying the number of classes or minimization, or maximizing the number of classes under certain restrictions. Introduction such restrictions necessary, because otherwise while minimizing the number of classes will be obtained a single class, and while maximizing the number of classes is obtained N classes. One such limitation can act parameter of similarity images. When parameter similarity, equal to unity, it is obtained N classes, when parameter similarity, equal or near to zero − one class. As a second constraint can act the presence or absence of ability to adapt weights of connections distributed recognition neurons.
In this regard, the dependence of the final result of learning a discrete network ART from sequence of presentation training images may be considered not as a drawback NN, but as its dignity, can create different classification at purposeful change input training sequence. Therefore, for discrete neural network ART-1 learning offers many new learning algorithms:
1. Training algorithms, in which the input image can not adapt weights of connections distributed recognition neurons after the resonance (used in noisy data):
1.1.
The learning algorithm of neural networks ART-1 the sequence of images, ordered by increasing values of their norm, wherein, the first to network are presented images with minimal norm. Applies in cases, when it is desired to obtain an increased number of classes of images.
1.2.
The learning algorithm of neural networks ART-1 the sequence of images, ranked by descending value of their norms, wherein, the first to network are presented images with the maximum norm. Applies in cases, when it is desired to obtain minimum number of image classes.
1.3.
The learning algorithm NN ART-1 the sequence of images, ranked by teacher, wherein in the training sequence can be used subsequence as with increasing, as with decreasing norm of the input images.
1.4.
The learning algorithm discrete neural network ART, in which the initial values of weights connections are given by teacher, using complex input images, which are derived from initial using Boolean operations "AND", "OR", "NOT", other mathematical operations, heuristics or combinations thereof forming methods of training images.
2. The learning algorithm, using a joint application of the algorithm rapid learning NN and learning algorithms without adaptation of network weights upon the occurrence of resonance.
An example of such algorithm can serve an algorithm, wherein in the first stage (first epoch) used the fast algorithm of neural network ART-1 learning, and at later epochs used learning algorithms without adaptation weights of connections recognizing distributed neurons of network upon the occurrence of resonance.
IV. ART NEURAL NETWORK FOR SOLVING PROBLEMS WITH MULTIPLE SOLUTIONS
A general lack systems of recognition and classification based on neural networks, including networks ART - obtain a unique solution, even in cases, when there are two or more possible and equivalent solutions. In recognition of such images recognition result may depend on the order of filing in the training mode reference pictures, given by teacher. Show it on the example.
Example 2. Recognition image, located on the borders of several classes.
Take ART-1 network with parameters: m = 5 – number Y-neurons in discriminating network layer; n = 12 – number of neurons in the input layer of the network; р = 0,5 – similarity parameter images.
Let the teacher used as reference the following three vectors: , who served in the training mode in the following order: .
Submission a neural network these vectors and calculation the equilibrium weights of connections from the formulas (1) leads to the following matrix weighting coefficients:
When the input of the neural network considered recognition mode vector then it will be assigned to the first class, that is, a single output signal will be on the output of recognizing neuron , because this neuron has a minimum index. If chosen neuron with maximal index, then the winner neuron became neuron . A similar situation arises when applied to the input neural network vector , which will be assigned to the second class because training image was filed before the image . To exit from this situation necessary to use a neural network ART, which ability to define multiple solutions (Fig. 1).
To extend the capabilities of discrete neural network ART-1 and get all the possible solutions of the problem of recognition to the basic architecture of ART-1 added another control neuron , the inverting outputs of the neuron R, and a recording neurons layer . Each neuron associated with binary unidirectional communication with the corresponding neuron .
Before recognition mode neurons translated into a passive state ties on the circuits, not shown in Fig. (1). Neurons , go to the active state by the rule "two out of three" - in the presence of single neurons of the output signals and control neuron . The unit output signal of the neuron through a feedback circuit fixes its unit output and inhibits neuron-winner .
After that, the network begins searching for a new neuron-winner. The search process continues until, until all recognizing distributed neurons not will inhibited. In this case on the outputs of neurons may not be no unit signal, since the input image not similar to any of the images, stored in the weights of network connections, or on outputs of -neurons may be one or more unit signal, respectively indicating belonging the input image to one or several classes of images.
CONCLUSION
Thus, it is developed a new architecture of discrete neural network adaptive resonance theory, which allows to specify one, two and an increasing number of decisions (if they exist) in pattern recognition and classification of black-and-white images.
Proposed new learning algorithms of discrete neural networks ART, prevent degradation and reproduction classes at training networks with noisy input data.
Overcome one of the drawbacks common classification systems based on neural networks, consists in the fact that it turns out only one classification, due to the method of teaching or raised by teacher. Proposed learning algorithms of discrete neural networks ART, allowing to obtain a variety of methods classifying input data.
CONFLICT OF INTEREST
The authors confirm that this article content has no conflict of interest.
ACKNOWLEDGEMENTS
Decleared none.


