Effect of Rotating Acoustic Stimulus on Heart Rate Variability in Healthy Adults
Abstract
Acoustic stimulus can modulate the Autonomic Nervous System. However, previous reports on this topic are conflicting and inconclusive. In this study we have shown, how rotating acoustic stimulus, a novel auditory binaural stimulus, can change the autonomic balance of the cardiac system. We have used Heart rate Variability (HRV), an indicator of autonomic modulation of heart, both in time and frequency domain to analyze the effect of stimulus on 31 healthy adults.
A decrease in the heart rate accompanied with an increase in SD and RMSSD indices on linear analysis was observed post-stimulation. In the Poincaré Plot, Minor Axis (SD1), Major Axis (SD2) and the ratio SD12 (SD1/SD2) increased after the stimulation. Post stimulus greater increment of SD12 with higher lag numbers of (M) beat to beat intervals, when compared to pre stimulus values, resulted in increased curvilinearity in the SD12 vs. Lag number plot. After stimulation,value of exponent alpha of Dretended Flactuation Analysis of HRV was found to be decreased. From these characteristic responses of the heart after the stimulus, it appears that rotating acoustic stimulus may be beneficial for the sympathovagal balance of the heart.
INTRODUCTION
Autonomic Nervous System (ANS) regulates the exchange of energy and information between the body and environment. A proper balance of the sympathetic and parasympathetic divisions of ANS is required for optimum functioning. A deviation from this balance is seen in diseases like Acute Coronary Syndrome, Diabetes and Heart Failure [1-3].
Sensory inputs, like auditory stimulus, can have a wide range of psychological and hemodynamic effects by modulating the ANS. Harmonic auditory stimulus has been shown to relieve stress and related ailments [4, 5]. Moving sound produced by the sequential excitation of a mono source through several speakers in a free field, can generate a specific activity in the brain [6]. It evokes a magnetic response in parietal and temporal cortex, which is not seen with a stationary sound stimulus [7, 8]. In order to facilitate such experimentation using moving sound we have previously engineered a binaural rotating acoustic stimulus [9].
Heart rate variability(HRV), a measure of the beat to beat fluctuation of the heart rate, is related to the functioning of the ANS. Due to its noninvasive nature and convenience of measurement, HRV is often used to assess the influence of ANS on cardiac function [10, 11]. Linear methods, analyzed in both time and frequency domain have been traditionally used to study HRV [12, 13]. However, such methods tend to ignore the complex and nonlinear nature of the cardiac system and potentially overlook vital information. Thus application of nonlinear methods like the Poincaré plot and the detrended fluctuation analysis (DFA) appears to be more appropriate. Poincaré plot analysis has been widely used as a quantitative –visual tool for HRV analysis [14-16]. A modification of this method, lagged Poincaré plot, has been shown to be a better quantitative tool for in some studies on Congestive Heart Failure (CHF) and Chronic Renal failure (CRF) subject populations [17, 18].
In this paper, we have studied the effect of rotatory acoustic stimulus on ANS by measuring HRV using linear and nonlinear methods.
RESULTS
For all measurements the ECG was recorded for 10 minutes each before and after exposure to the stimulus with a gap of 10 minutess after the end of the stimuli. Only sinus beats were selected for analysis. In the linear analysis of HRV, the mean heart rate decreased from 83.1±per minute to 81.8± per minute after the exposure to the stimulus. The decrease was more in subjects with higher baseline heart rate. Both the standard deviation (SD) of R- R interval i.e the time interval between R- peak of two continuous sinus beats and the root - mean -square differences of successive R- R interval (RMSSD) increased after exposure to the stimulus. SD value changed from 23.7± 2.9 ms to 26.8 ± 2.5 ms and RMSSD value changed in a similar fashion from 21.8± 3.2 ms to 23.8 ± 3.3 ms. All the changes were significant with paired t test value < 0.05.
We used lagged Poincaré plot analysis, a scatter plot of RRn and RRn+M(RRn-time difference between two successive R peaks, RRn+M- time difference between the next Mth successive R peaks), as one of the non linear methods. When this plot is adjusted with an ellipse three important parameters are obtained namely SD1, SD2, and SD12 (SD1/SD2). SD1 is the length of the semi-minor axis of the ellipse and SD2 is the length of the semi-major axis [18]. In this analysis, with an increase in the lag number the plot became more scattered with an increment in the length and width of the plot (Fig. 1A, 1B). This effect was more pronounced post stimulation. Also, the center of the plot shifted to a higher value indicating a decrease in heart rate.
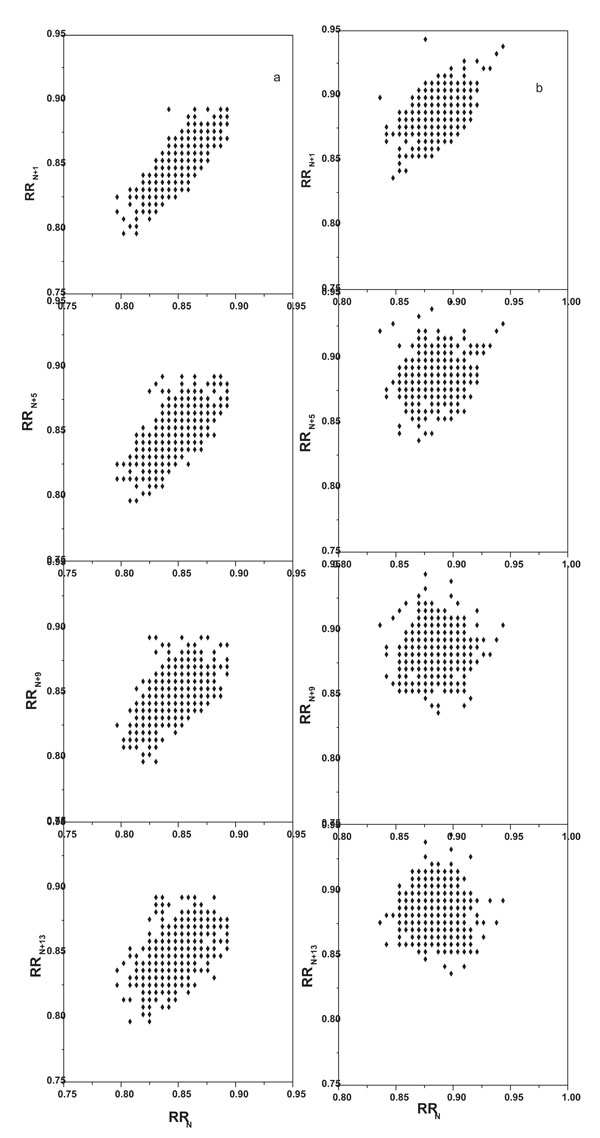
lagged Poincaré plot from a representative individual A: Pre stimulation, B: Post stimulation. From top to bottom panel- lag number 1, 5, 9, 13 respectively.
Average values of parameters SD1, SD2 and SD12 increased significantly post-stimulation (p-value <0.001). The rate of increase in SD1 with an increase in lag number (M) was higher. The increment in SD12 value post-stimulation also increased with an increase in lag number. (Fig. 2A, 2B). These results indicate that rotating acoustic stimulus enhances both short and long term correlation of heart beat.
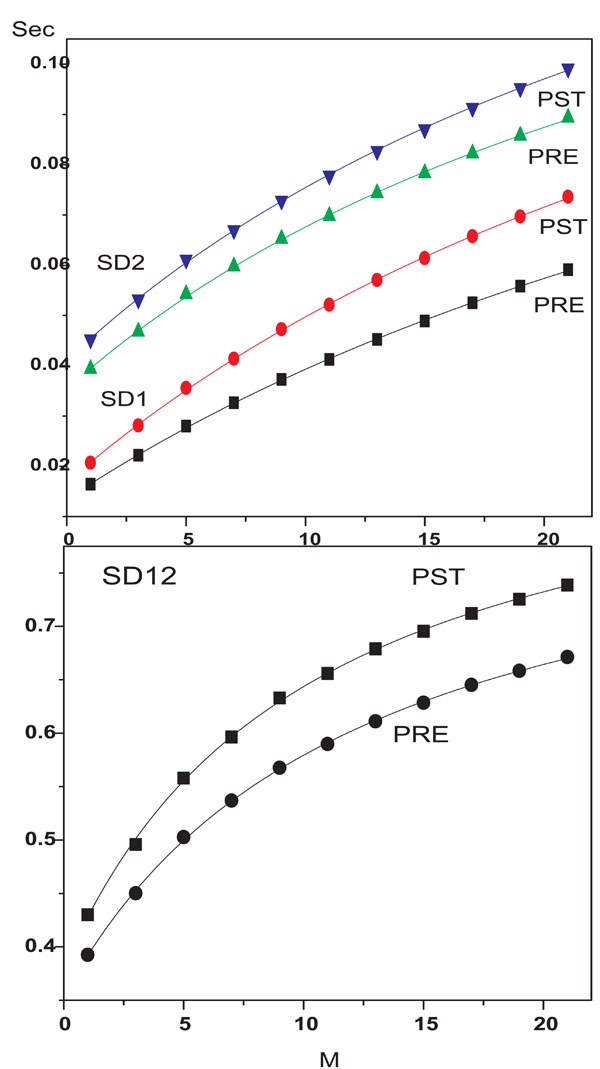
Changes in average values of SD1, SD2 (A) and SD12 (B) with an increase in lag number (M).
Pade Approximant method was used to find out the relationship of these parameters with the lag number M. We assumed a simple form of the Pade approximant for SD’s as the ratio of polynomial in M of degree one.
Here Y = SD1, SD2 or SD12 and χ = a/c, β = b/a and γ = d/c. Latter parameters were taken as new unknown parameters. An excellent fitting of the data with the equation (1) (Fig 2A, 2B) was found with different set of χ, β and γ which were listed in Table 1. When expressed for small lag number M the equ.(1) can be approximated as Y = C + L M + Q M2 where L = χ ( β - γ) and Q = γ L. Such variation of these parameters for small M has been found earlier [17]. The values for L and Q have been shown in Table 1. The magnitude of slope and curvature of SD1 increased post-stimulation. The ratio SD12 exhibited a larger change in both slope and curvature due to stimulation. The post stimulation value of the curvature of SD12 is increased by 51% whereas that of the slope is augmented by 27%. On the other hand only the linear coefficient for SD2 increased after the stimulation. The corresponding values of L and Q for individual subject are shown in Fig. (3A, 3B). The slope and magnitude of curvature increased for the majority of subjects post-stimulation.
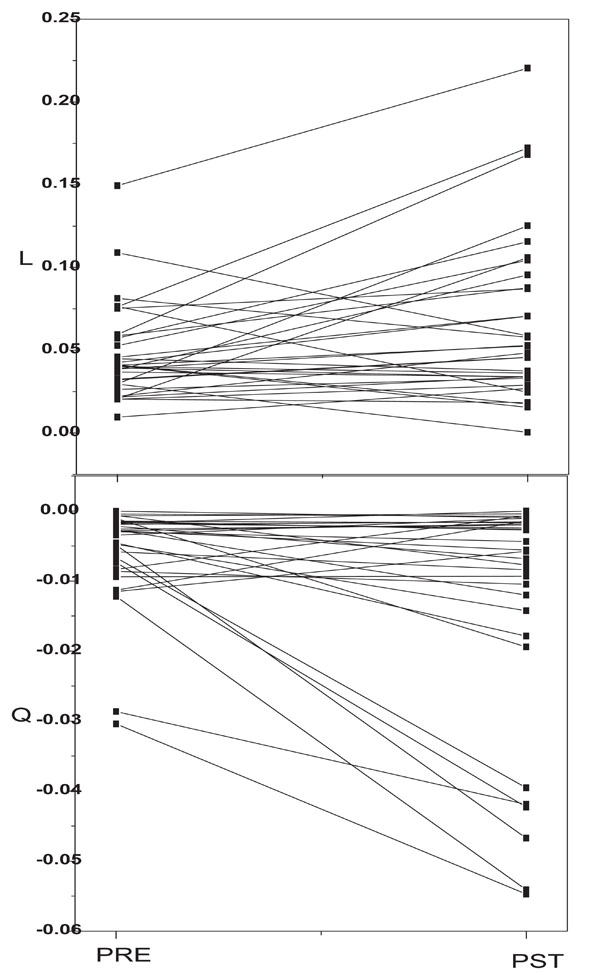
The corresponding values of L(A) and Q(B) for individual subject before and after stimulation.
The Value of Parameters χ, β ,γ Obtained from Fit of eq.(1) with Respective Value of R2. The Parameters L and Q are the Coefficient of Linear and Quadratic Terms in Expansion of Y in Terms of M.
| SD1 | SD2 | SD12 | ||||
|---|---|---|---|---|---|---|
| PRE | POST | PRE | POST | PRE | POST | |
| χ x10-2 | 1.34 | 1.68 | 3.54 | 4.11 | 35.38 | 38.03 |
| β x10-2 | 25.52 | 27.25 | 15.07 | 13.74 | 19.93 | 23.58 |
| γ x10-2 | 2.15 | 2.56 | 3.12 | 2.94 | 8.27 | 9.84 |
| χ2 x10-6 | 0.04 | 0.06 | 0.08 | 0.1 | 3.04 | 7.02 |
| R2 x10-2 | 99.99 | 99.98 | 99.98 | 99.7 | 99.97 | 99.95 |
| Lx10-3 | 3.14 | 4.14 | 4.23 | 4.44 | 41.1 | 52.2 |
| Q x10-4 | -0.067 | -1.06 | -1.32 | -1.31 | -34.1 | -51.4 |
The other non linear method we used was the detrended fluctuation analysis (DFA) [16]. The coefficient α, derived from the DFA and its distribution for subjects are plotted in Fig. (4A and 4B) respectively for pre- and post- state of stimulation. The stimulation produced a decrease in the coefficient α for most of the subjects and mean for the group decreased. The mean of α for group changes from ± to ± after the stimulation with a p value of 0.003.
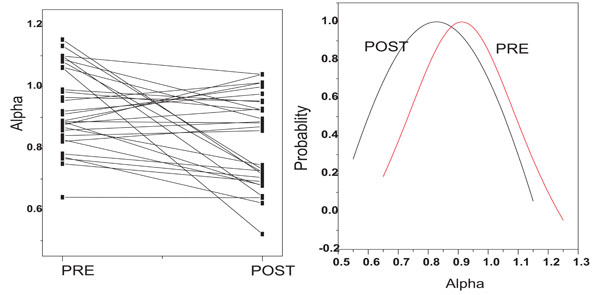
Changes in coefficient α (A) and its probability distribution (B) for pre- and post- state of stimulation.
DISCUSSIONS
In the present study we have shown that rotating musical stimulus influences the autonomic nervous system. We have previously shown that rotating acoustic stimulus significantly decreases arousal in psychosomatic patients [9]. This is the first study showing standardized rotating musical stimulus can influence the autonomic nervous system, based on analysis of the Heart Rate Variability. Rhythmic acoustic stimulus has been shown to exert modulatory effects on the cardiovascular system, gastric motility and response of an individual to aversive stimulus [19-23].
However the mechanism behind this hasn’t been clearly elucidated with some studies implicating autonomic nervous regulation [24, 25] while others showing no changes in ANS activity [20, 23]. These studies have been limited by small sample size, use of non standardized sound stimulus, stationary nature of the stimulus and lack of non linear analysis to study HRV [20, 26].
In this study linear analytical components of HRV like SD, RMSSD were shown to be increased post stimulation. SD, RMSSD are considered as measures of parasympathetic tone of the heart [27]. Earlier studies have established decreased SD as an independent predictor of mortality and sudden death in chronic heart failure. Lower SD, RMSDD are associated with more frequent and complex arrhythmia in right insular infarct patients [28-31]. So, increment of SD and RMSSD after the rotating acoustic stimulus suggests a potentially beneficial effect on the cardiovascular functioning. It alters the autonomic balance in a favorable direction without causing an overall down regulation of the whole cardiac system, indicated by the individual increment in SD, RMSSD.
SD1 is the reflection of short term variability of heart rate and is mainly influenced by the parasympathetic division of ANS. SD2, the length of the semi-major axis, is the measure of long term variability. Lagged Poincaré plot analysis showed a significant increase in SD1, SD12 with higher lag numbers post stimulation thus indicating an increase in parasympathetic modulation. Previous studies with HRV analysis using Lagged Poincaré plot have shown a decrease in Vagal modulation (SD1, SD12) with exposure to hazardous stimulus like smoking and disease conditions like diabetes [32, 33]. So, it can be argued this post stimulus improvement in parasympathetic modulation, measured by SD1, SD12, is a favorable outcome of the stimulus.
A curvilinear relation has been seen in previous studies between lag and Poincaré plot indices of heart rate variability and this curvilinearity has been shown to be impaired in disease conditions like CHF. An increase in the same has been proposed to be associated with improved cardiovascular functioning and outcomes in CHF patients on therapy [18]. In our study, an increase in curvilinearity was observed in SD1 and SD12 with higher lag numbers post stimulation indicating a positive modulation in cardiovascular function mediated by improvement in the parasympathetic control on the heart. Here we would like to mention, we have used Pade approximant method for the first time to quantify the parameters of lagged Poincaré plot. It is a simple and illustratory method to assess the change in cardiovascular response and have added some new dimensions to the lagged Poincaré Plot. It helped in identifying the slope and curvature of the lag plot separately.
Detrended Fluctuation Analysis has shown the long-range power law correlation of the RR interval time series in normal subjects and in other physical systems. Value of exponent alpha of DFA was reported to be of higher value in congestive heart failure patients when compared to normal subjects [16]. In our study we have found that the mean value of exponent alpha of DFA is lower after the stimulation. This also may be considered as an indicator for an improved functioning of cardiovascular system.
At the end, we suggest that rotating acoustic stimulus improves parasympathetic tone, which is beneficial for cardiac functioning. It shows statistically significant changes of the HRV parameters. However, one of the limitations of this study was that results obtained were immediate reflection of the stimulus. To assess the duration of the effect of rotating acoustic stimulus on ANS would be an interesting follow up, which was beyond the scope of this study.
CONCLUSIONS
Rotating musical stimulus causes acute changes in cardiac autonomic regulation resulting in an increase in the parasympathetic activity. The changes observed in the Linear and lagged Poincaré plot indices are predictors of favorable cardiovascular outcomes indicating a potentially beneficial effect of the stimulus. These findings are encouraging and warrant more studies in selected patient population to identify a potential therapeutic application of this stimulus.
MATERIALS AND METHODS
Stimuli
A rotating musical stimulus, constructed from an Indian percussion instrument tabla, was used for the study. The stimuli were recorded digitally at a sampling rate of 44.1 kHz in 16 bit. The stimuli were given in a sound proof room with the subjects in recumbent position. Headphones connected to a computer through a custom electronic interface were used to deliver the stimulus binaurally. The sound was played at around 50 db (peak value) for 9.5 mins ensuring an optimum perception by subjects. A perception of moving sound was created by varying its amplitude in both ears. The ear receiving higher amplitude sound perceived the stimulus to be moving towards it whereas the ear receiving lower amplitude sound perceived it to be moving away. The amplitude of sound was modulated at a frequency of 2 Hz with a phase difference of 0.568 seconds between the advancing and receding stimuli. We have also tried frequencies lesser or greater than 2 Hz and we found that the perception of rotation of sound is at maximum for 2Hz [9]. The final perception produced was that of a rotating sound moving in plane passing through ears and perpendicular to body axis. No subject experienced nausea, vertigo or decreased arousal during or after exposure to stimuli. All experiments were conducted at a fixed time to avoid any Diurnal Variation on HRV.
Subjects and Measurements
Thirty one subjects (11 male; 20 female; average age 36 ±12 yrs) were included in the study after an informed consent. Exclusion criteria for the study included any current disease condition, ongoing medication regimen and any history of cardiac, neurological, psychiatric or sleep disorder. The study was approved by the ethical committee of IIT Kharagpur, India. Electrocardiographic (ECG) data was taken from three limb leads of the patient in supine position with a sampling rate of 500 Hz and a resolution of 12 bit. ECG was recorded for 10 minutes each before and after exposure to the stimulus with a gap of 10 mins after the end of the stimuli. Only sinus beats were selected for analysis. R-R interval, defined as the time interval between the R peaks of two continuous sinus beats, was detected through the Origin software. Nonlinear analysis of HRV was done using Matlab Software and a standard program was used for linear analysis.
Data analysis
The Task Force guidelines of HRV analysis (Task Force of the European Society of Cardiology and the North American Society of Pacing and Electrophysiology) were strictly followed in our study [34].
Linear Analysis
HRV was assessed in time domain. In linear time domain the heart rate (HR), standard deviation (SD) of RR interval, root-mean squared successive differences (RMSSD) were calculated.
Non Linear Analysis
Poincaré plot is a scatter plot of RRn and RRn+1( RRn-time difference between two successive R peaks, RRn+1- time difference between the next 2 successive R peaks) . When this plot is adjusted with an ellipse three important parameters are obtained namely SD1, SD2, and SD12 (SD1/SD2). SD1, the length of the semi-minor axis of the ellipse, is the standard deviation of beat to beat variability in the RR interval. SD1 is the reflection of short term variability of heart rate and is mainly influenced by the parasympathetic division of ANS. SD2, the length of the semi-major axis, is the measure of long term variability [35].
In lagged Poincaré plot, the ellipse was fitted to the Poincaré plot of RRn+M vs RRn where M is the lag number. SD1 and SD2 were calculated for lag M from the relation : SD1 = [Ф(M) -Ф(0)]1/2 and SD2 = [Ф(M) + Ф(0)]1/2 . Where the auto-covariance function Ф(M) was given by Ф(M) = [34].
The long term correlation in RR–time sequence was assessed by Detrended Fluctuation Analysis The measure of correlation was given by a scaling exponent (α) of the fluctuation function F(τ) ≈ τα. The computation of fluctuation function F(τ) was done in the following way. For a given time sequence R(ti), ti = iδt where δt is characteristic time interval for the sequence and i=1, N, an integrated time series r(ti) was defined as r(ti) =∑ij [R(tj) – Rm], i=1, N where Rm was the mean of R(ti). The integrated series was divided into boxes of equal size of time τ =n δt and linear function was used to fit box data. The fluctuation function F(τ) was calculated as root mean square fluctuations relative to the linear trend. The power law behavior of F(τ) provided the scaling exponent. It has been observed that acceptable estimate of the scaling exponent α (from DFA) can be obtained from analysis of data sets of length 256 samples or greater (equivalent to approximately 3.5 min for RR data at a heart rate of 70 bpm). The analysis of RR data for period of 10 min time interval was therefore expected to provide an adequate measure of the scaling exponent [16, 36, 37].
CONFLICT OF INTEREST
The authors confirm that this article content has no conflicts of interest.
ACKNOWLEDGEMENTS
The authors gratefully acknowledge the Biomedical Signal analysis group, Department of Applied Physics, University of Kuopio, Finland for allowing us to use HRV software, Dr S. Mazumdar for his critical comments on the manuscript and Mr S. Ghosh for his technical help.


