Dissociation of Exact and Approximate Calculation in Severe Global Aphasia
Abstract
We report a 68-year-old patient with severe global aphasia secondary to a large left hemisphere infarction including the parietal lobe. In addition to language and neuroradiological evaluation, the patient was given specifically designed arithmetic and clock tasks requiring either exact calculation or approximate calculation. Despite severe language impairment, the patient showed relatively well-preserved abilities for numerical comprehension and arithmetic operations. Further analyses using specifically designed arithmetic and clock tasks demonstrated a clear dissociation of the patient’s abilities between impaired exact calculation and well-preserved approximate calculation. The results support the notion that numerical and arithmetic abilities are heterogeneous in that rote verbal arithmetic facts and quantitative numerical knowledge can be separable. Implications of the present findings for neural correlates of numerical and arithmetic processing suggest that the right hemisphere plays a crucial role in approximate calculation.
INTRODUCTION
Language is well recognized to contribute importantly to numerical and arithmetical processing, as evidenced by clinical observations that most aphasic patients have difficulty with such tasks. However, some patients have been reported to show well-preserved arithmetic and numerical processing despite severe deficits involving general intelligence and/or language abilities [1, 2]. In contrast, Denes and Signorini [3] reported a patient with severe impairment of numerical processing and arithmetic while language was only slightly affected. In addition, Anderson et al. [4] reported a patient who demonstrated dissociation between reading numerals and other letters. These clinical observations suggest a hypothesis that numerical and arithmetic processing is carried out at least partially independently of general language processing.
Patients with aphasia and acalculia may show dissociation in performance reflecting qualitative differences between arithmetic operations [5-11]. In addition, two patients with “pure anarithmetia” reported by Dehaene and Cohen [12] demonstrated dissociation between tasks requiring rote verbal arithmetic facts and those requiring quantitative numerical knowledge. Based on these findings, various arithmetic operations may not share an identical neural circuit. Rather, each operation appears to be subserved by multiple distinct but mutually related information processing pathways.
Studies concerning the neural basis for numerical and arithmetic processing have emphasized the importance of the left inferior parietal lobule. However, recent functional neuroimaging studies [6, 13-15] as well as precise lesion analyses in neuropsychological case reports [12] have provided evidence that arithmetic operations are subserved by several different neural networks connecting different brain areas.
We evaluated a patient who showed relatively well-preserved abilities for numerical comprehension and arithmetic operations despite severe global aphasia resulting from a large left hemisphere lesion including the parietal lobe. The patient demonstrated an intriguing dissociation between exact and approximate arithmetic. The results provide useful insights concerning neural correlates of numerical and arithmetic processing.
CASE REPORT
A 68-year-old, right handed woman with no family history of left handedness sustained cerebral infarction in November 20xx, resulting acute right hemiplegia and language deficits. After diagnosis and initial treatment at another hospital, she was transferred to our hospital in March 20xx+1 for further rehabilitation. On admission, neurological examination disclosed persistence of severe right hemiplegia. Neuropsychological examination disclosed global aphasia, ideomotor, ideational, and buccofacial apraxia, and visuoconstructional deficits. Further language evaluation demonstrated that spontaneous speech was limited to a few very common words such as “yada” (no) and “teiuka” (rather). The patient was unable to produce any other meaningful words. Confrontation naming, repetition, and reading aloud were impossible; responses with partial completion were noted. Verbal comprehension was severely impaired even in everyday conversation. Correct choice of the appropriate word from two alternatives presented auditorily or visually occurred at a chance level only.
In contrast to the severe language deficits, verbal comprehension of numerals was relatively spared even from the beginning. From money on a table she was able to pick up an amount equal in value to a verbally announced sum. She was able to carry out actions at a given time by watching a clock; moreover, her family as well as the nursing staff concluded that she was aware of appointments although she did not explicitly refer to them. Arithmetic performance as evaluated with the Western Aphasia Battery (WAB) was 3/3 for simple addition tasks and 2/3 for simple subtraction tasks. However, the patient was unable to read or write numerals.
T2-weighted magnetic resonance imaging (MRI) on March 21, 20xx+1 demonstrated a large area of high signal intensity including almost all of the left middle cerebral artery territory (Fig. 1). At the same time point, 99mTc-ECD single-photon emission computed tomography (SPECT) demonstrated significant hypoperfusion of the entire left hemisphere (Fig. 2).
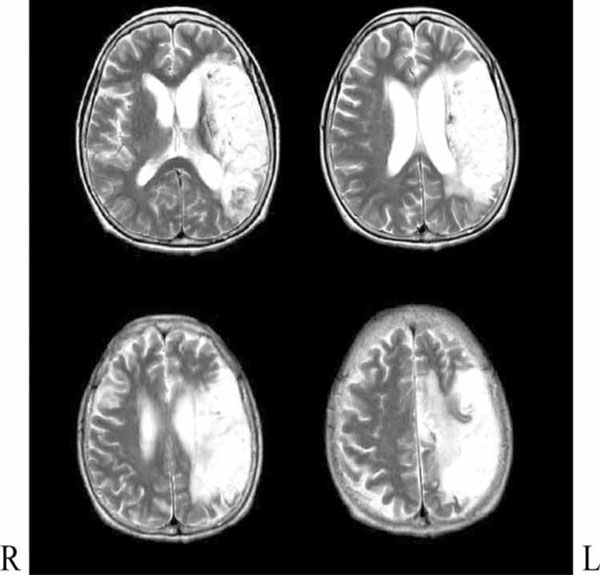
Magnetic resonance imaging demonstrated a large lesion in the left middle cerebral artery territory.
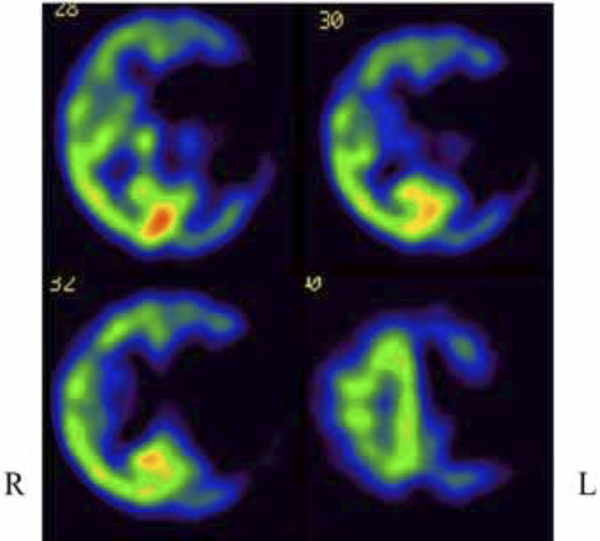
Single-photon emission computed tomography demonstrated hypoperfusion specially corresponding to the lesion shown by magnetic resonance imaging.
The patient’s comprehension of numerals was analyzed further as follows.
Quantitative Comprehension of Numerals
The patient was asked to pick up a number of tokens as indicated by auditorily presented numbers or visually presented numerals. The correct response rate was 7/10 for auditory presentation and 10/10 for visual presentation.
Auditory - Visual Number Matching
The patient was asked to point out the Arabic numeral that corresponded to an auditorily presented number. The correct response rate was 7/10.
Chinese Number - Arabic Numeral Matching
The patient was asked to respond by pointing to the number on a list of 10 Chinese numbers that corresponded to a given Arabic numeral. Performance of the opposite task also was tested, pointing to the Arabic numeral among 10 that corresponded to a given Chinese number. The correct response rate was 10/10 for both tasks.
Numerical Semantic Knowledge
The patient was asked to answer visually presented multiple-choice questions concerning numerical knowledge such as number of days in a year and number of days in a month. The correct response rate was 5/5.
Comparison of Two Numbers
The patient was requested to point out the greater of two numbers visually presented as numerals. The correct response rate was 73/80.
Thus, the patient showed relatively well-preserved abilities for numerical comprehension and arithmetic operations despite severe global aphasia. To analyze her arithmetic processing we further compared performance of exact and approximate arithmetic.
METHODS
Arithmetic Task
According to Stanescu-Cosson et al. [13], the patient was given 20 questions requiring use of one of three rules of arithmetic, i.e., addition, subtraction, or multiplication. Division was not tested because the patient refused solving the problems. The patient was asked to respond by pointing to one of two alternatives presented on a white card. Two conditions were set; exact calculation (E) and approximate calculation (A). Under the E condition (Fig. 3a), the wrong answer was close to the exact correct answer by 2-3 units. In contrast, under the A condition (Fig. 3b), the approximate correct answer was a number off by only one unit, and the wrong answer was remote from the correct one (Fig. 3b). E and A conditions for each arithmetic operation were tested twice on separate days. Operands ranged from 1 to 9. Questions re-using the same digit (e.g. 2+2, 6+6) were avoided.

Examples of the E (exact) condition (panel a) and the A (approximate) condition (panel b) for arithmetic tasks.
Clock Task
Two versions of this task were devised. In a digital-to-analog task, the patient was asked to respond by pointing to the one among four alternative analog clocks that indicated the time shown digitally. In the analog-to-digital task the patient was requested to do the opposite, i.e., to choose one of four digital clocks corresponding to an analog clock. For each clock task E and A conditions were set as in the arithmetic task. In the E condition both correct and wrong answers were shown in minutes (e.g., 12: 37, 8: 57), while in the A condition answers were shown as full or half hours (e.g., 6: 00, 12: 30). Twenty questions for each condition of the two clock tasks were given to the patient.
RESULTS
Arithmetic Task
For addition, performance under E condition was significantly worse than under the A condition [E, 19/40 correct (47.5%) vs. A, 36/40 correct (90.0%), chi2=16.81, df=1, p<.0001]. Similar results were obtained for subtraction with performance under the E condition being significantly worse [E, 17/40 correct (42.5%) vs. A, 33/40 correct (82.5%), chi2=13.65, df=1, p<.0002]. For multiplication, however, correct responses were similarly limited to a chance rate of occurrence under E and A conditions [E, 20/40 correct (50.0%); A, 19/40 correct (47.5%) correct, chi2=0.05, df=1, p>.10] (Fig. 4).
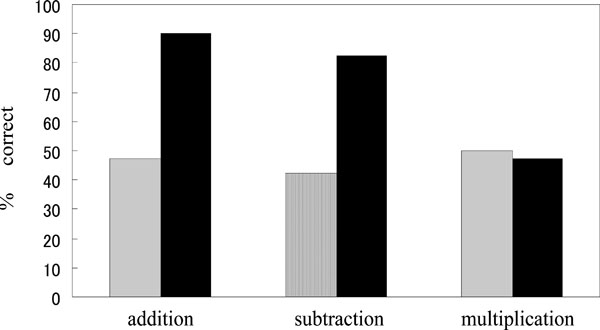
Results of the arithmetic task. Performance under the A condition (filled columns) was significantly better than under the E condition (open columns) for addition and subtraction tasks. In contrast, performance of multiplication was similarly poor under A and E conditions. A, approximate; E, exact.
Clock Task
For both the digital-to-analog and analog-to-digital tasks, performance under the E condition was significantly worse than under the A condition [digital-to-analog for E, 3/40 correct (7.5%) vs. A, 35/40 correct (87.5%), chi2=51.33, df=1, p<.00001; analog-to-digital for E, 17/40 correct (42.5%) vs. A, 36/40 correct (90.0%), chi2=20.18, df=1, p<.00001] (Fig. 5).
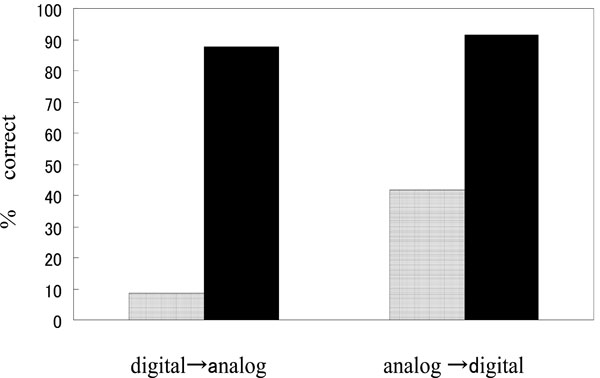
Results of the clock task. For both digital-to-analog and analog-to-digital tasks, performance under the A condition (filled columns) was significantly better than under the E condition (open columns). A, approximate; E, exact.
DISCUSSION
Numeric and Arithmetic Processing
In an analysis of numerical and arithmetic processing, Dehaene and Cohen [7] postulated two distinct pathways involving symbolic and magnitude representations (Fig. 6). The symbolic representation deals with arithmetical operations, transcoding (reading and writing) and memory for digits. Verbalization is essential for symbolic manipulation. In contrast, magnitude representation transfers information from digital to analog form without verbalization, and plays a major role in estimation or comparison of quantities, memory for magnitude, and approximate measurements.
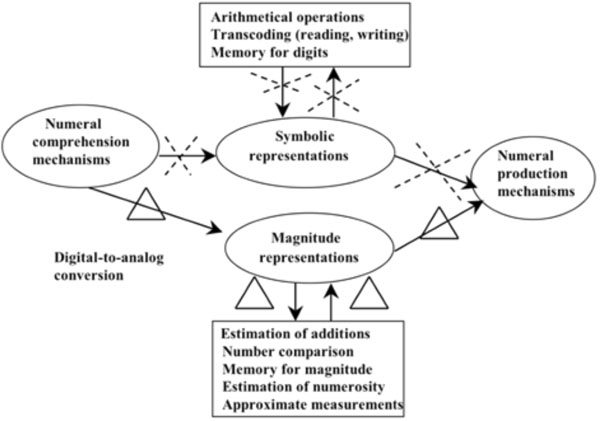
Diagram of information processing for numerals and arithmetics as proposed by Dehaene and Cohen [7], with apparent functional lesions shown for the present patient.
The present patient had severe language deficits, that interrupted symbolic representation processing of numericals and arithmetic operations. Specifically, the patient showed great difficulty with multiplication under both E and A conditions, and with addition and subtraction under the E condition. According to the above model of Dehaene and Cohen [7], the patient’s symbolic representation pathways appeared to have been disrupted for connecting numeral comprehension to numeral production via any route of arithmetical operations and for transcoding (reading and writing)(dotted Xs, Fig. 6).
On the other hand, the patient showed well-preserved addition and subtraction under the A condition, and also, performed well under the A condition in the clock tasks. These findings suggest that the patient retained ability to estimate quantities provided that mathematical manipulation and transcoding were not involved. More precisely, a pathway (triangles, Fig. 6) that connects ‘digital-to-analog representations’ via magnitude representation partially supported her numerical abilities and enabled her to compare magnitudes and arrive at estimated answers and approximate measurements.
Dehaene [16] further revised their symbolic and magnitude representation model to result in a triple-code model, in which Arabic numbers and quantity representation could be processed in both hemispheres while processes requiring access to verbal formats could be subserved only by the left hemisphere. Accordingly, the four rules of arithmetic may involve different types of information processing. Our patient demonstrated dissociated performance between A and E conditions for addition and subtraction, while multiplication showed equally impaired results under both conditions. The results suggest that the patient retained ability to use only arithmetic rules that do not require verbal formats.
Neural Substrates of Numerical and Arithmetic Processing
As demonstrated by MRI and SPECT, our severely aphasic patient had a large left hemisphere lesion. A natural interpretation of the results would be that her well-preserved magnitude representation system was subserved by the right hemisphere. Recent activation studies performed in healthy normal subjects partially support this notion. Dahaene et al. [14] reported that the left hemisphere was activated by multiplication, while comparison of number magnitude produced activation in the right hemisphere. In addition, in functional MRI experiments with a similar paradigm including both A and E conditions in normal arithmetic processing, Dehaene et al. [15] and Stanescu-Cosson et al. [13] demonstrated left-sided activation under the E condition but right-sided activation under the A condition. Results for the present patient, who was severely aphasic and had a large left-sided lesion, thus are consistent with the results obtained by functional neuroimaging in normal subjects. Studies on a split-brain patient further supported a dissociable role of right-left hemispheres for calculation. Funnel et al. [17] reported that the right hemisphere does have some capacity for approximating the solution even when it is unable to generate the exact solution. Although it is hard to further locate the precise neural substrate for approximate calculation within the right hemisphere, a recent fMRI study given to a patient with acalculia has found a significant role of the angular gyrus on the right side [18]. Specifically, anterior parts of the right angular gyrus are supposed to be crucial for automatic calculation.
Importantly, Dehaene [16] concluded that addition is processed in the right hemisphere while subtraction is processed in both hemispheres. If this hypothesis is correct, subtraction may be less impaired by lateralized brain damage than addition. However, subtraction was no better than addition in the present patient. The large size of the patient’s lesion could account for the apparent disagreement. Numerical and arithmetic processing normally may involve the right and left hemispheres together, while processing was severely restricted in the right hemisphere in the present patient.


